Travail et énergie potentielle de pesanteur - Énergie mécanique

L'étude d'énergie Mécanique nécessite des connaissances avancées en relation avec la notion du travail d'une force (constante) , l'énergie cinétique ainsi que l'énergie potentielle de pesanteur.

Avant d'entamer la série d'exercices ,Nous vous conseillons vivement de consulter les ressources du cours .

Exercice 1 : l'énergie mécanique d'un corps solide en mouvement.

Au sommet d'un planche incliné, de longueur $AB=7m$, un corps $(S)$ est abandonné sans vitesse initiale .

Au cours du mouvement, les forces de frottement sont négligeables et l'angle d'inclinaison $\alpha =30^{0}$.

Nous considérons le niveau du plan horizontal passant par B, comme référence de l'énergie potentielle de pesanteur,la masse du corps $m=1kg$ et $g=10N/kg$

1- Quelle est l'énergie mécanique du corps au sommet.

2- En appliquant le théorème de l'énergie cinétique, Déterminer la vitesse $V_B$ du corps lorsqu'il atteint la position B.

3- Calculer l'énergie mécanique en B.

la mesure de la vitesse en B donne la valeur : $V’_B=8m/s$.

4- Calculer l'énergie cinétique obtenue expérimentalement à la position B : $E'_{c}(B)$.

5- En déduire la nouvelle énergie mécanique en B.

6- Justifier l'existence d'une force de frottement d'intensité f (à déterminer),

Correction Exercice 1 : Energie mécanique

1)- L'énergie mécanique est donnée par l'expression : $E_m=E_{pp} +E_C$

Comme $E_C(A)=0$ et $E_{pp} (A)=m.g.AB.sin(\alpha)$

Alors : $E_m = 35j$

2)- Le théorème de l'énergie cinétique : $\Delta E_C =E_C(B) - E_C (A) = W(\vec P)_{ A\to B}$

Soit alors : $\frac{1}{2}.m.V_B^2 = m.g.AB.sin(\alpha)$ donc $V_B =\sqrt{ 2.g.AB.\sin(\alpha)}$=8,36(m/s)

3) Sachant que B est situé au plan de référence de l'énergie potentielle de pesanteur , alors $E_{pp}(B)=0$ , l'énergie mécanique se réduit à l'énergie cinétique du corps.

$E_m(B)=E_C(B)= \frac{1}{2}.m.V_B^{2}= 35j$

4)- On sait que $E'_C (B)=\frac{1}{2}.m.V_B^{2}$ , soit alors : $E'_C (B)= 32j$

5)- Même raisonnement que la question 3 ,On obtient : $E'_m(B)=32j$

6)- Nous observons une dégradation au niveau de l'énergie mécanique entre le point de départ et le point d'arrivé B : $\Delta {E_{m}}_{A\to B}\mathopen\lt0$. Pas de conservation de l'énergie mécanique associée au corps, nous écrivons alors $\Delta {E_{m}}_{A\to B}= E'_m(B)- E_m(A)=W(\vec f)_{A\to B}=-f.AB$

Donc $f=0,43N$ .

Exercice 2 : l'énergie mécanique d'un skieur

Un skieur relève le défi d'atteindre une hauteur $H=10m$ du sol. pour ce faire il se lance d'une vitesse $V_A=10m/s$ sur la piste AC comportant une portion rectiligne AB ,et un quart de cercle BC de rayon $R=4m$.

Nous assimilons le skieur à un point matérielle de centre d'inertie G, et on néglige l'effet de frottements au cours du mouvement. le niveau du sol est pris comme origine d'énergie potentille de pesanteur.

Données : la masse du skieur $m=70kg$ ,On prend $g=10N/Kg$.

1- Vérifier que l'énergie mécanique du skieur en B est $E_m(B)=a=3,5(kj)$.

2- Par application de la conservation de l'énergie mécanique , montrer que la vitesse en un point M, repérer d'un angle $\theta$ (la figure) est donnée par la forme: $$V_M =\sqrt{\frac{2.a}{m} - 2.g.R[1- cos(\theta)]}$$

3- En déduire la valeur de la vitesse du centre d'inertie du skieur lorsqu'il atteint la position C.

4- En appliquant la conservation de l'énergie mécanique, Justifier l'échec de la tentative.

5- Quelle est la vitesse minimale de lancement pour atteindre l'altitude H.

En se déplaçant, le skieur subit une force de friction (force de frottement) supposée constante le long de la piste AC.

6- Calculer à nouveau , la vitesse de départ $V_A$ sachant que l'intensité associée aux forces de frottements est $f=10N$ et $AB=10m$.

Correction Exercice 2 : énergie mécanique d'un skieur

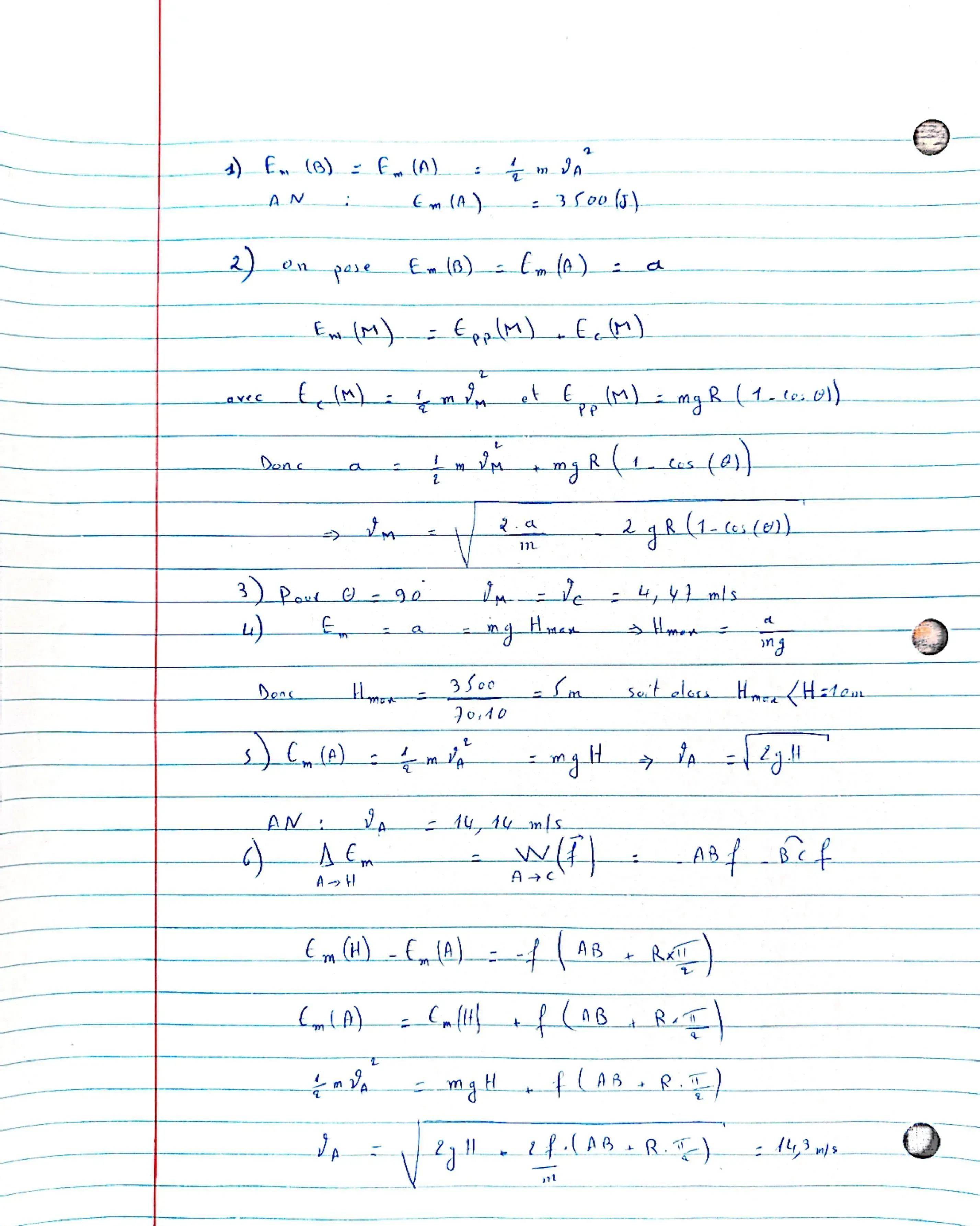
Exercice 3 : Énergie mécanique d'une tige homogène

Une tige métallique homogène de masse $m=0.5Kg$,d'une longueur AB=L, susceptible de tourner autour d'un axe fixe $(\Delta)$,on abandonne le système $(S)$ sans vitesse initiale à partir d'une position repérée d'un angle $\theta_i=80^0$ par rapport à l'axe vertical passant par l'axe de rotation.

1- Donner l'expression de l'énergie potentielle de pesanteur de la tige en fonction de L,$\theta $, $m$ et $g$.

Lorsque $\theta =0$,le centre d'inertie G est confondu avec $G_0$.Nous prenons le plan horizontal passant par $G_0$ comme référence de l'énergie potentille de pesanteur .

2- Exprimer l'énergie mécanique de la tige à $\theta =0$.

3- Par conservation de l'énergie mécanique, trouver la valeur de la vitesse angulaire $\omega $ de la tige pour $\theta_0=0$.

4- Quelle est la valeur de l'énergie mécanique de la tige pour un angle $\theta=45^0$,En déduire l'énergie cinétique.