Systèmes Mécaniques Oscillants -Pendule

Série d’exercices corrigés : Oscillateurs mécaniques - pendule élastique , simple et de torsion

Exercice 1 : étude d’un pendule élastique sur un plan horizontal

L’exercice propose l’étude dynamique et énergétique d’un pendule élastique en mouvement horizontal sur un plan.

On considère le système oscillant {ressort- solide(S) } formé d’un ressort de masse négligeable de constante de raideur notée K, et un solide de masse m=0,4g susceptible de se déplacer sans frottement sur le plan horizontal.

Le système est en équilibre, le centre d’inertie du système se confond avec l’origine du repère terrestre (galiléen) $R(O,\vec{i})$,On écarte alors le solide (S) d’une distance notée $x=d$ par rapport à l’origine du repère.

A un instant considéré comme origine des dates le solide est libéré sans vitesse initiale.

Partie 1 : étude dynamique

1. à un instant donné t, faire l’inventaire des forces extérieures (la représentation des forces est nécessaire).

2. Montrer que l’équation différentielle vérifiée par l’abscisse x s’écrit sous la forme : $$\ddot{x}+\frac{K}{m}.x=0$$

3. On admet la forme $x(t)=X_{m}.cos(\frac{2\pi.t}{T} +\phi)$comme solution de l’équation différentielle, trouver l’expression de $T$.

La figure ci-contre, représente l’évolution de l’abscisse occupé du centre d’inertie G du solide au cours d’oscillation en fonction du temps.

4. A partir de la figure trouver la valeur de K et $X_{m}$ l’amplitude maximale de l’oscillateur.

Partie 2 : étude énergétique de l’oscillateur (pendule élastique).

On prend le plan horizontal qui passe par le centre d’inertie du solide comme référence de l’énergie potentielle de pesanteur, on considère que l’énergie potentielle élastique associée au ressort est nulle lorsque le système est en équilibre.

5. Donner à un instant t , l’expression de l’énergie potentielle élastique $E_{pe}$ ,l’énergie potentielle de pesanteur $E_{pp}$ associée au solide. En déduire l’expression de l’énergie mécanique du système {ressort- solide(S) }.

6. Lors des oscillations, l’énergie mécanique du système se conserve, Calculer la vitesse $V_{0}$ lorsque le solide passe par l’origine du repère.

Exercice 2 : pendule élastique en mouvement vertical, oscillation verticale

Un ressort est attaché à un mobile (S) de masse m, le système est alors en position d’oscillation verticale sans frottement autour d’une position d’équilibre, voir la figure.

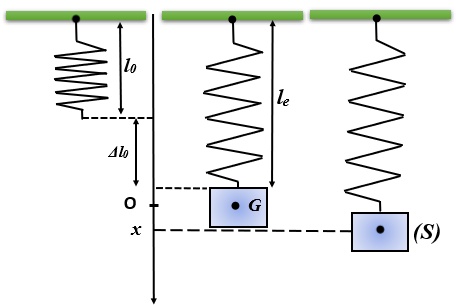
1. La longueur à vide du ressort est notée $l_{0}$ , en position d’équilibre la longueur du ressort prend la valeur $l_{e}$ .

1. Donner l’expression de la tension associée à la tension du ressort.

2. En appliquant la première loi de Newton ,établir la relation entre les grandeurs : m , g , $Δl_{0}$ et k la constante de raideur du ressort.

3. En décale le corps (S) vers le bas, et on le lâche sans vitesse initiale, en appliquant la deuxième loi de newton établir l’équation différentielle suivante :$$\ddot{x}+\frac{K}{m}.x=0$$

Lorsque le système est en équilibre, l’énergie potentielle élastique $E_{pe}=0$ et on considère le plan horizontal qui passe par l’origine est une référence de l’énergie potentielle de pesanteur.

4. Donner l’expression générale de l’énergie potentille de pesanteur lorsque le centre d’inertie G du système occupe la position d’abscisse x.

5. L’expression générale de l’énergie potentielle élastique a la forme :$E_{pe}=\frac{1}{2}.k.\Delta l^{2} +C$ ,déterminer la constante $C$.

6. Montrer que l’énergie potentielle totale du système s’écrit sous la forme :$E_{p}=\frac{1}{2}.k.x^{2}$

7. Que peut-on dire de l’énergie mécanique du système, retrouver l’équation : $$\ddot{x}+\frac{K}{m}.x=0$$

Exercice 3 : pendule élastique sur un plan incliné

Sur un plan incliné on attache un ressort de constante de raideur k à un support fixe, l’autre extrémité est attachée à un solide (S) de masse m. lorsque le système est en équilibre, le ressort s’allonge d’une distance $Δl_{0} $ .

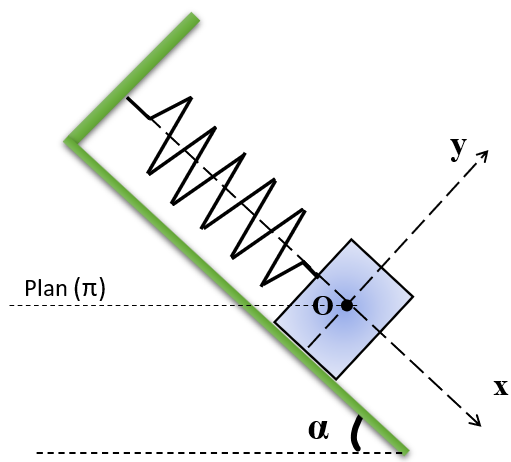
Partie 1 : étude à l’équilibre.

1- Montrer la relation à l’équilibre :$\Delta l_{0}=\frac{mg.sin(\alpha)}{k}$ .

Partie 2 : étude dynamique .

On écarte le corps et on le lâche sans vitesse initiale, le mouvement est alors oscillatoire , sans frottements.

2- Trouver l’équation différentielle vérifiée par l’abscisse

Partie 3 : étude énergétique.

On prend l’énergie potentielle élastique nulle à l’équilibre, le plan horizontal (\pi) comme référence de l’énergie potentiel de pesanteur.

3- Donner l’expression de l’énergie cinétique du système.

4- Trouver l’énergie potentille du système.

5- Etablir l’équation différentielle des oscillations.